Almost seven years ago I tweeted this:
Fast forward several years, one on-going pandemic including sanitized groceries, and we have revived the “Estimation Station” as a school-wide mathematics activity. Here’s how we are doing it!
Continue reading
Almost seven years ago I tweeted this:
Fast forward several years, one on-going pandemic including sanitized groceries, and we have revived the “Estimation Station” as a school-wide mathematics activity. Here’s how we are doing it!
Continue readingIt’s the start of a new school year and one of my personal goals this year is to get back into blogging. Reflection is a key part of my pedagogical practice and this blog serves that purpose. Another reason is that we are in the beginning stages of a research project in which blogging and journaling will be part of the data collection process. So I’m following the advice of my good friend, Carl Oliver, and just pushing send.
Well not quite yet, I will at the end of the post. I promise. But, before I do push send, I wanted to discuss one of the most vulgar, wicked, fiendish, and ear-splittingly foul four letter words in the educational lexicon, time. Teachers and students are constantly asking for more time for a variety of things. How often have we heard things like: “I need more time to finish the problem.” “I need more time to assess the students.” “I need more time for self-care.” Time is at a premium in education and everyone is looking for how to maximize it.
To illustrate this point, I’d like to share a story. This year I am working with a new assistant teacher and she has just begun her educational career. We began the year by using John Stevens’ Would You Rather instructional routine. Our plan was to use this routine as a warm-up and then move on to another activity, however the lesson she had created was going so well that we decided to continue it with an extension that asked the students to create their own Would You Rather prompts. Afterwards, she asked me why we didn’t move onto the next activity as planned and the only phrase that I could think of was, “Cost Benefit Analysis.” In our classroom to support students with a variety of disabilities, we try to focus solely on the goal of the lesson. The goals of this lesson were for students to think critically, explain, justify, and express themselves. Teachers make an average of 4 instructional decisions every minute and each of those choices should be in service of the instructional goal of the lesson. So each decision is analyzing the cost of time with the potential benefit towards the instructional goal. This instructional routine was allowing students to construct viable arguments and critique the reasoning of others while also providing us, the teachers, with some valuable formative assessment of their mathematical skills and levels of thinking. The benefits far outweighed the cost of scrapping the other planned activity. (Sorry Dan!)

I am also often asked about levels of prompting and how much support teachers should provide students with disabilities. The answer is another cost-benefit analysis. Factors to consider in your cost-benefit analysis are the needs of the student, the cost of independence and the potential benefit towards the instructional goal of the lesson.
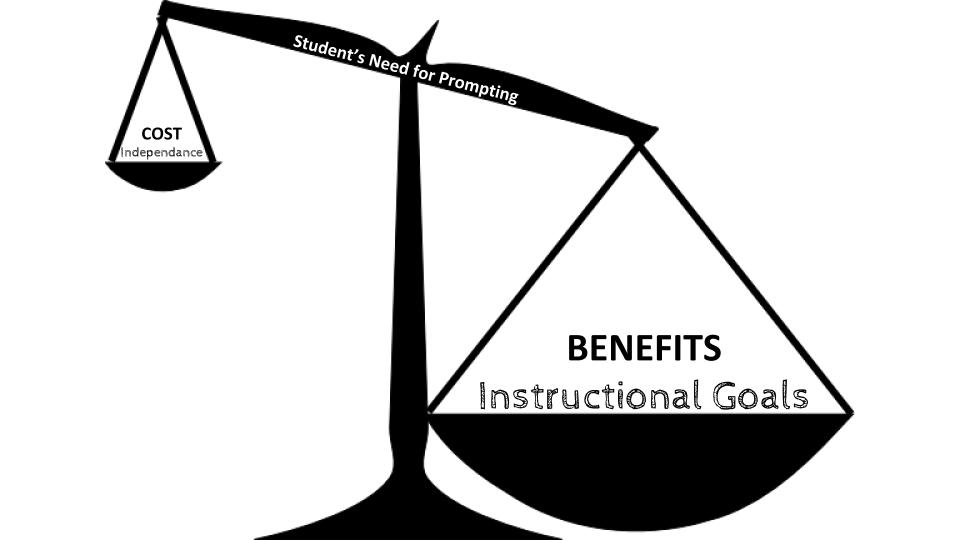
Our speech & language therapists facilitated a professional development session on how the levels of prompting relate to language input and output. They created and shared this graphic that everyone found very useful.

To alleviate the gravity of each of these cost-benefit analyzed instructional decisions, we implement instructional routines as a way to “temporarily hold some things [in the classroom] constant while working on others.” So of the 270,000 decisions that my assistant teacher and I will make this year hopefully, as David Wees states, instructional routines allow us to focus our decision-making on the most important things, the students and the math.
Sent!

Since its inception in 2015 as a rogue addition to the National Council of Teachers of Mathematics (NCTM) Annual Meeting and Exposition in Boston, ShadowCon has provided teachers, teacher leaders, and academics with inspiration and motivation through the intriguing and passionate calls to action presented by educators of every stripe.

Michael Pershan at ShadowCon15
In the inaugural event, Laila Nur, Tracy Zager, Elham Kazemi, Kristin Gray, Michael Pershan, and Christopher Danielson presented their calls to action that spanned from giving the right kind of hints to solve math problems to using your sense of humor to create a safe and enjoyable space for your students in math class.
The talk that I gravitated towards in 2015 was Tracy Zager’s Breaking the Cycle. Zager, author of Becoming the Math Teacher You Wish You’d Had, contrasts how elementary school teachers describe mathematics with the descriptions of mathematicians. Spoiler alert: the mathematicians’ descriptions are drastically more positive. I was inspired to share word clouds Zager created with my colleagues after I asked them about their own opinions of mathematics. I also felt motivated to engage with Tracy and other educators around the country on the ShadowCon website.

Brian Bushart and me at ShadowCon16
The next year, at the 2016 NCTM Annual Meeting and Exposition in San Francisco, I was asked to be a live tweeter for Brian Bushart‘s fantastic #ShadowCon16 talk called, Make Your Own Kind of Music. The presence of live tweeters is an important innovation established by ShadowCon hosts Dan Meyer, Mike Flynn, and Zak Champagne in order to provide live access to as many people as possible, even those who are not in attendance but who can witness the event live on twitter.

ShadowCon18 speakers and hosts from left to right: Mike Flynn, Me, Nanette Johnson, Lauren Lamb, Dan Meyer, Javier Garcia, Zak Champagne
This year, at the 2018 NCTM Annual Meeting and Exposition in Washington DC, I had the privilege to be invited to speak at #ShadowCon18! Instead of reading a description of my talk entitled, “Presume Competence: Don’t Leave Your Expectations At the Door, Raise Them!” Watch it for yourself!
Go ahead, I’ll wait…

Thanks for coming back! Now that you’ve watched my talk you’re probably so ready to presume the competence of your students, but you may be wondering what to do next.
This is how ShadowCon is unlike any other conference experience. Each speaker from this year’s event will be continuing the conversation via email to delve deeper on the subject of their talk. Go to bit.ly/shadowcon18 to signup for one of these #ShadowCon18 email threads. The speakers will be sending discussion prompts, activities, and reflections to each email thread over the next month or so.
Last week, we had our first parent/teacher conferences of the school year. During the conferences we discussed the importance of self-advocacy for students with disabilities, that mathematical proficiency is more than procedural fluency, and how hard it can be for a parent of a student with a disability. This time afforded me the opportunity to reflect on some of the reading I’ve done lately including some books more specifically about disability.

One such book is Disability Studies and the Inclusive Classroom by Susan Baglieri and Arthur Shapiro. Baglieri and Shapiro present an easily digestible version of how disability is currently situated in the world of education and society. Baglieri and Shapiro go into detail about two models of disability that influence our work with students with disabilities in the school setting. They are the medical model and the social model of disability.
This blog post was co-written with Rachel Lambert and available on both blogs.

A couple of years ago, Rachel Lambert and myself were talking about how students in special education are conceptualized. We were sick of hearing about the “gaps” and the “holes” in our student’s learning. One of us, (probably Rachel!), blurted out – “Our students are not Swiss cheese!” We laughed, since this summed up for us how learners with disabilities are both over-analyzed and under-educated, always seen as the sum of their deficits, not their strengths. What follows are two recent experiences we’ve each had in which the idea of thinking of students as Swiss cheese has resurfaced.
There are many ways to start the school year in math class, some are better than others. Building a culture of risk-taking, mistake-embracing, hard-working, respectful students who view themselves as mathematicians is no small feat.
When trying to instill a risk-taking, mistake-embracing culture. I find it helps to make mistakes yourself! #MTBoS #Iteachmath #SwDMathChat pic.twitter.com/c5PYjWjiZl
— Andrew Gael (@bkdidact) September 19, 2017
Why is this important? Because research says that the way student’s view themselves in math class can predict future attainment levels in math class. Also, developing a productive disposition towards mathematics is a key to any student’s success in school. So should we focus on developing classroom norms or beginning the year with math tasks? Tracy Zager, author of Becoming the Math Teacher You Wish You’d Had, weighs in.
Whether we choose to start the year by jumping into a rich task on the first day, or by engaging in a reflective study about what it means to do mathematics, or by undertaking group challenges and conversations to develop norms for discourse and debate, we must be thoughtful about our students’ annual re-introduction to the discipline of mathematics.
So this year in order to re-introduce our students to math, we developed a collection of activities specifically chosen not only to engage students meaningfully in mathematics, but to also develop a productive disposition to mathematics as well. Continue reading
The weeks after the NCTM Annual Meeting and Exposition are usually a time of personal professional reflection and consideration about the future direction of the organization itself.
During Congressional recess, Senators and Representatives go back to their communities and hold town halls to hear the issues that are important to their constituents.
In Tracy Zager‘s recent blog post reflecting on her own experience at the NCTM conference, she says the following [emphasis added]:
From where I sit, the merger with The Math Forum, the emphasis on #MTBoS representation on all NCTM committees, the MTBoS keynote in Nashville, and the support of our fringe events like Game Night and ShadowCon are meaningful. I’m all for pressing NCTM to be what we need it to be. But I’m also all for recognizing the big shifts made over the last few years. Change comes faster within the (unstructured, unregulated) #MTBoS than it can within the (highly structured, institutionalized) NCTM, just by the nature of the beasts. But good change is happening nonetheless.
The blog post you are reading right now focuses on the idea of “#MTBoS representation on all NCTM committees.” Recently, Carl Oliver, Tina Cardone, and I began two-year terms on the NCTM Publishing committee. Our first committee meeting will be held soon and we’ll all have more specific information afterwards, which we’ll be sure to share. So, in an effort to begin with transparency, this particular post is meant to be a kind of digital town hall.

As #MTBoS constituents, please share your answers to these (or other questions) in the comments section…
To be completely honest, as #MTBoS committee representatives we cannot promise to address everything, but we’d like to begin this adventure knowing what’s already on YOUR mind!
Today, we celebrated our belated Pi Day! It was delayed due to inclement weather…

Though my #MTBoS friends were there to comfort me in my time of need!
@bkdidact that’s the rounded up version anyway, none of this truncated 3/14 crap
— Jonathan (@rawrdimus) March 13, 2017
Our spring trimester focus is always financial literacy. So, we spent most of last week researching recipes, planning for a shopping trip, going to the bank, shopping for ingredients, and making pies. Yes, I said it. We made pies for Pi Day, sue me! Now, finally the time had come to eat our pies, but first…we had to do some more math!
First we reviewed of some of the digits of Pi, highlighting that when rounded to the nearest hundredth it matches the numerical date of March 14th, which is subsequently known as “Pi Day” for this reason. I also wore my Pi shirt, which gives the students an opportunity to see that there are A LOT of digits in this number known as Pi and that I’m a nerd. We did, however, skip the traditional digit memorization activity for several reasons including working memory and tedious boredom.
Instead we estimated, explored, and discovered the circumference formula with our pies and some string.
Continue readingThis blog rarely veers into discussions of national education policy, but after the events of last night’s confirmation hearing for the Secretary of Education nominee, that time has come.
The nominee, Betsy DeVos, is an advocate for school choice (pro and con). Essentially, she believes that federal education dollars should follow students to the schools they choose to attend (public, private, religious, charter, etc.) and not directly to the schools through state funding. Senator Michael Bennet of Colorado summed up some of the pitfalls of school choice, “There’s no practical difference between being forced to go to a terrible school and [choosing] between five terrible schools.” As a teacher of students with disabilities in a private institution, I understand that not all public school settings are appropriate for every student. However, I am personally against the dismantling of public education in favor of privatization.
One aspect of the hearing that struck me, as an advocate for students with disabilities, was DeVos’ lack of understanding of the Individuals with Disabilities Education Act (IDEA). When asked about it directly by Virginia Senator Tim Kaine, this was the exchange that followed:
Should the rights of students with disabilities be left up to the states? Should we be taken back to a time when students with disabilities were excluded from education in favor of exclusionary special classes or, worse, institutionalization? The correct answer to that question, if you were still on the fence, is no.
However, evoking such a dark time in our country’s past, such as Willowbrook, may seem hyperbolic, but when a nominee for the highest education job in our nation displays a staggering ignorance of a federal law which protects the rights of an often neglected population of students, well, nothing seems too unrealistic to consider. We must consistently grapple with the follies of the past in the hopes of not repeating them.
IDEA is important because it explicitly protects the rights of students with disabilities to a free and appropriate education (FAPE) in the least restrictive environment where all stakeholders, especially the students and their families, give input on how to best meet the student’s educational needs. To mistake or be unaware of this federal law is unforgivable. Period. And as Senator Maggie Hassan of New Hampshire, whose son has cerebral palsy, said “It’s not about sensitivity, although that helps. It’s about being willing to enforce the law so that my child, and every child, has the same access to high-quality public education.”
UPDATE [1/19/17]: Senator Maggie Hassan discusses IDEA and Betsy DeVos with Chris Hayes on MSNBC
We are currently studying geometry. The standards for geometry list one important understanding to develop before 4th grade, “Reason with shapes and their attributes.” If you click through the link you can read more about the specifics, but the activity that gets students reasoning about shapes and their attributes the most, in my opinion, is Which One Doesn’t Belong? This activity allows students to share their thinking about shapes and their properties without the fear of being wrong. Why? Because every answer is correct as long as you can justify your reasoning! You can read more about how I implement “Which One Doesn’t Belong?” in my class and you can use it for more than just geometry.
But this post is about how I used this activity as a basis for an instructional routine. Continue reading
The Blog of a K-8 Math Specialist
Innovative math lessons you can use in your classroom today
Trying to find math inside everything else
Inspire, Connect, Reflect
Reflecting about education...almost always about math!
Learning from our most powerful teachers : children and one another.
Rachel Lambert's work on math + disability resources
A place to talk about teaching and learning
Ramblings of a HS Math Teacher
learns and observes
Helping all to find their inner math nerd, even if you didn't know you had one.
Making Math Sense
Learning about learning and teaching mathematics.
Lover of math. Bad at drawing.
a community for number string design
I research mathematics teaching and learning in secondary schools
A Weekly Digest of the Mathematical Internet
Fun missions & prompts, Always ready! Blogging initiation starts Jan 2017
Lighting the world with math, one student at a time.
mathematics + music
Integrating Technology and Mathematics
thoughts on education by Grant Wiggins
Kassia Omohundro Wedekind
A View From the Schoolhouse
Megan Schmidt's Reflective Blog about teaching, mathematics, and sometimes beagles.
a work in progress
My place to write about teaching, and math, and teaching math.
teaching, math, teaching math
Creating wonder in the rabbit hole called School--Mary Dooms
Better through reflection
Reading and writing about math education
Reflections on teaching and parenting young mathematicians
I have no idea why I picked this blog name, but there's no turning back now